Unplanned cycle ride and Python

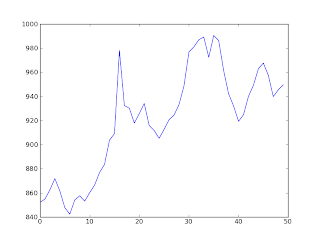
Around May 2011, the time I decided to go on solo bike rides and GoogleMaps has been of great help ever since. It was only after a few months, I realized there was a python binding for GoogleMaps. Only after going on an unplanned solo cycling trip recently, I realized how much of a help it can be. Since most of the times I'm on highways and well raid roads, it is possible to get the elevation of the whole route. When the elevations are plotted, it gives a vague idea of the terrain. On the left the terrain of road from Channarayapatna to Hassan (Elevation is in mtrs).

Enough talk and here is the code. The elevation api has been used to get elevation of a point and googlemaps api has been used to get the latitude and longitude of start and end points. The points along the route have been interpolated as of now. But they can be obtained point by point using googlemaps api and interpolated based on the distance.

Will probably do all that and make another post soon. Happy coding till then.

Enumerating Palindromic Numbers

A palindromic number remains same when reversed. Ex: 141, 5, 22, 1991, 27472 and so on..

I came across a problem which needed me to check if a number is a palindrome which I can do by reversing the number and comparing it with the original.

But what if I wanted all the possible palindromic numbers of a given width.

If I wanted all the 5 palindromic numbers, I can solve them by considering the number as abcba where a, b, c are digits and a!=0. The number would be a(10000) + b(1000) + c(100) + b(10) + a.

Then the problem becomes trivial.

for a in range(9, 0, -1):
  for b in range(9, -1, -1):
      for c in range(9, -1, -1):
          num = 10001 * a + 1010 * b + 100 * c

But as we can see, it is not generic and making it generic this way, would require me to use iterators.

On a sunday morning, travelling from Krishnagiri to Dharmapuri in a local bus, at 04:14, this sweet and simple approach occured to me.

It is a recursive approach that considers the fact that all n digit palindromes can be generated by adding a digit at the front and back of the (n - 2) digit palindromes and (n - 4) digit palindromes and so on.

Ex: 5 digit palindromes are of the form
a***a where a != 0 and *** is a 3d palindrome
a0*0a where * is a 1d palindrome.

def nDigitPalins(n):

    if n == 1:
        return range(9, 0, -1) 
    elif n == 2:
        return [11 * x for x in range(9, 0, -1)]
    else:
        p_zeros = [i * (10 ** (n -1) + 1) for i in range(9, 0, -1)]

        p = []
        for base in p_zeros:
            for y in range(1, (n + 1) / 2):
                for subPalin in nDigitPalins(n - 2 * y):
                    p_num = base + subPalin * (10 ** y)
                    p.append(p_num)
            p.append(base)

        return p

print nDigitPalins(8)

You can run the code at http://ideone.com/szO5q

is perfect square

How do you write a program that checks if a number is perfect square or not.

def isPerfectSquare(x):
    i = 0
    while i * i < x:
        i += 1
    return i * i == x

This is such a beautiful code.

Is it??? How about this.

def isPerfectSquare(x):
    xRoot = int(x ** 0.5 + 0.1)
    return xRoot * xRoot == x

or in my favourite lambda way,

isPerfectSquare = lambda x: int(x ** 0.5 + 0.1) ** 2 == x

If you know what is going on, you'll love the recipe. If you don't then start thinking.